课程简介

分形几何展示了数学之美，它能让人们感悟到科学与艺术的融合、数学与艺术审美的统一。

教学目标

使用scratch画出分形图，学会递归函数的使用

教学重点

基本图形的画法，递归函数的调用

教学过程

问题描述：

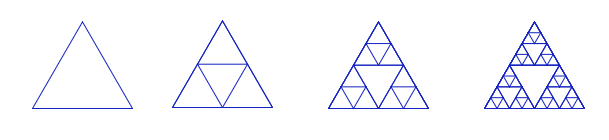
谢尔宾斯基三角形是最经典的分形图之一，它由波兰数学家谢尔宾斯基在1915年提出。如图是一个在平面内绘制的谢尔宾斯基三角形的分形图案，它由许多个大小不等的等边三角形构成。

谢尔宾斯基三角形的画法如下：

（1）画一个等边三角形，并沿三条边中点的连线将它分为4个小三角形。

（2）排除中间的一个小三角形，对其余3个小三角形再执行4等分的操作。

（3）重复上述步骤，可以得到更多、更小的等边三角形。最终这些大小不同的等边三角形就构成了谢尔宾斯基三角形。

编程思路：

根据上述算法绘制谢尔宾斯基三角形的编程思路和步骤。

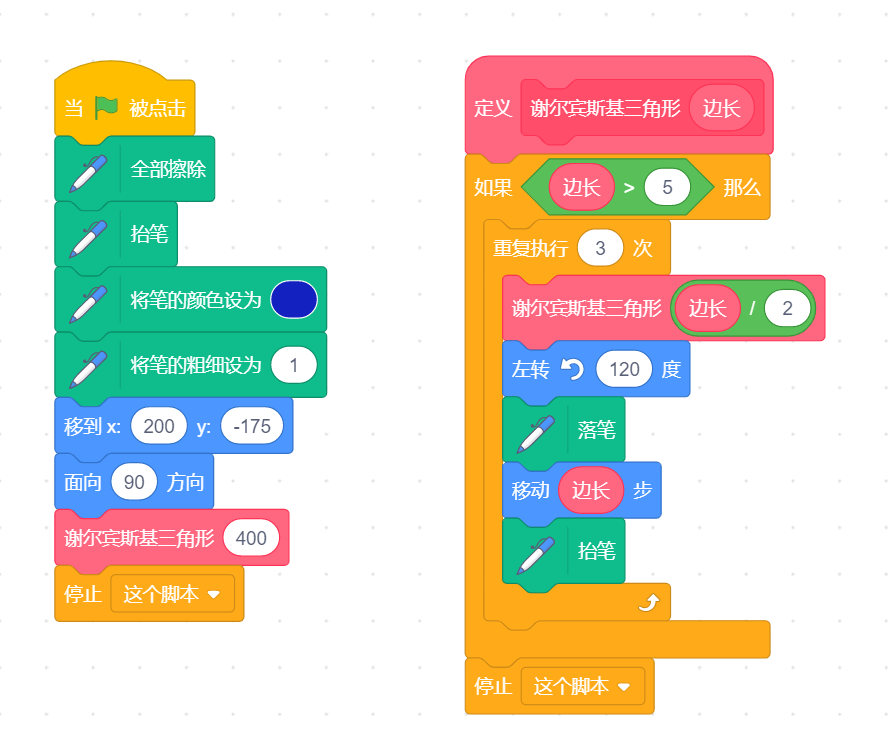
（1）画出基本形状。这个分形图的基本形状就是一个等边三角形。首先创建一个名为“谢尔宾斯基三角形”的模块，参数为“边长”，是要绘制的等边三角形的边长。然后在一个“重复执行……次”的循环体内依次向左旋转120°画出一个等边三角形。

（2）使用递归方法画出完整的分形图。分形图通常使用递归方式绘制，它可以使绘制过程变得非常简单。在代码中的“重复执行3次”循环指令内部的第一行加上递归调用，指令是“谢尔宾斯基三角形（边长/2）”。另外，将递归的终止条件设置为边长小于或等于5.通过调整这个数值，可以控制以递归方式绘制的三角形的数量。

（3）在入口程序中，设置画笔颜色和大小、角色的初始方向和位置，以及调用“谢尔宾斯基三角形”模块。

程序清单：

试一试：

稍加修改程序，画出彩色的谢尔宾斯基三角形。